I was recently in Princeton for the program committee meeting of the POPL conference. It was a lot of fun. David Walker, the program chair, offered excellent leadership, and I am excited about the program that we ended up selecting. I look forward to seeing many of you at the conference (Mumbai, January 2015).
POPL is a broad conference, and you really feel this when you attend its PC meeting. You inevitably discuss papers with fellow PC members whose backgrounds are very different from your own. Of the papers discussed, there are many that use techniques about which you only have rudimentary knowledge.
One thing I kept wondering at the meeting was: is POPL really one research community? Or is it really a union of disjoint sets of researchers who work on different themes within POPL, for example types or denotational semantics or abstract interpretation? Perhaps researchers in these sub-communities don’t really work with each other, even if they share a vision of reliable software and productive programming.
The question was bugging me enough that I decided to try to answer it through an analysis of actual data. The results I found were intriguing. The takeaway seems to be that POPL is indeed one family, but not a particularly close one.
Methodology
The concrete questions that I wanted to investigate were:
- How closely connected is the POPL community? As in, suppose you construct a collaboration graph where nodes represent POPL authors, and edges link authors who have co-authored a POPL paper. Or alternatively, suppose you built an overlap graph where nodes are POPL papers with multiple authors, and edges connect papers that share one or more authors. What do these graphs look like?
- Specifically, are the graphs made of a few disjoint components?
- Are there prominent clusters of authors who publish POPL papers together, or clusters of papers that are written by a subcommunity of researchers?
Note that the collaboration graph and the overlap graph are closely related. A node in the overlap graph — a paper — corresponds to a clique, consisting of the paper’s authors, in the collaboration graph. This means that the overlap graph is an abstraction of the collaboration graph, and you can easily construct the latter from the former. However, the overlap graph is easier to visualize because it has fewer nodes and cliques, and because of this, I will mostly focus on this graph in the rest of this post.
The bibliographic database DBLP offers a giant XML file that contains Bibtex listings for all papers ever published in major venues in computer science. To answer my questions, I wrote a Python script that analyzes this file and creates an overlap graph and a collaboration graph for POPL. To make sure that the graphs capture the current state of the community, I restricted myself to POPL papers from the period 2005-2014.
Next I used the Python package NetworkX to analyze the overlap graph. In particular, I generated the graph’s connected components, which correspond to disjoint sub-communities of POPL. I then ran some further transformations and analyses on the largest of these components.
The giant connected component
What I found to be a massive surprise is that the overlap graph has a “giant” connected component. This component contains authors from a wide variety of subfields, including types and semantics and model checking and abstract interpretation. What this suggests is that while POPL authors take many different technical approaches, POPL has not splintered into multiple communities – ideas from different groups move among those in the community.
More precisely, the overlap graph that I generated has 333 papers, written by 760 unique authors, and 96 components. However, 186 papers are part of a single connected component! In contrast, the second largest component only contains 6 papers. The 5th largest component has only three.
What’s interesting is that the giant component has a pretty large diameter: 18. Also, the average shortest path length between two nodes is 5.41. In fact, when you look at the collaboration graph, the latter number becomes 6.27 (for comparison, the corresponding number for the Facebook network is 4.74). This means that the maxim of six degrees of separation applies to the POPL network as much as others. This also means that POPL isn’t quite a tightly connected family.
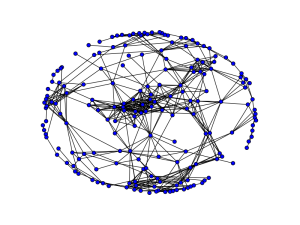
Here’s the giant component in the overlap graph (click for a bigger image). You can see that the component still has some clear “communities” in it. My next question was whether we could identify those communities.
Communities
To find author communities, I ran a “community analysis” algorithm on the largest component in the overlap graph. The community analysis is parameterized by a positive integer k. Technically, it computes a k-clique community: the union of all cliques of size k that can be reached through “adjacent” k-cliques, where two k-cliques are adjacent if they share (k – 1) nodes. The algorithm is based on a method called clique percolation.
Interestingly, this algorithm doesn’t give great results when applied to the collaboration graph. Think of two papers with authors {A,B,C, D} and {C, D,E, F}. The community-finding algorithm would report these two as separate communities, as they are 4-cliques that do not share 4 – 1 = 3 nodes with each other.
On the other hand, the overlap graph for this scenario will have two nodes connected by an edge. Applied to this graph, the community-finding algorithm will report a community made of the two nodes — surely a better-quality result.
Running on the POPL overlap graph, the community-finding algorithm was able to discover many interesting collaboration patterns. For instance, I found a 5-clique community centered around me, and containing my Ph.D. advisor, my first Ph.D. student, and some of my current collaborators.
The largest community I found for any value of k (actually, k = 12) is made of papers by these authors:
Peter W. O’Hearn; Cristiano Calcagno; Hongseok Yang; Thomas Dinsdale-Young; Lars Birkedal; Philippa Gardner; Matthew J. Parkinson; Byron Cook; Eric Koskinen; Maurice Herlihy; Richard Bornat; Viktor Vafeiadis; Alexey Gotsman; Suresh Jagannathan; Mike Dodds; Gavin M. Bierman
Viva la separation logic!
And here are the authors from the second-largest community:
Justin Hsu; Marco Gaboardi; Arjun Narayan; Andreas Haeberlen; Alan Schmitt; J. Nathan Foster; Michael B. Greenwald; Jonathan T. Moore; Benjamin C. Pierce; Alexandre Pilkiewicz; Aaron Bohannon; Eijiro Sumii; Michael Greenberg; Stephanie Weirich; Catalin Hritcu; Delphine Demange; David Pichardie; Arthur Azevedo de Amorim; Randy Pollack; André DeHon; Nathan Collins; Andrew Tolmach; Arthur Charguéraud; Brian E. Aydemir; Daniel Wagner; Martin Hofmann
I spot the Penn PLClub!
Here’s another entertaining fact. The center of a graph is the set of nodes that are, well, central. Formally, the center is the set of nodes whose maximum distance to other nodes in the graph is minimal. The center of the overlap graph consists of these two papers:
Contextual effects for version-consistent dynamic software updating and safe concurrent programming. By Jeffrey S. Foster, Michael Hicks, Polyvios Pratikakis, and Iulian Neamtiu. POPL 2008.
A Combination Framework for Tracking Partition Sizes. By Tal Lev-Ami, Mooly Sagiv, and Sumit Gulwani. POPL 2009.
Every paper in the largest component is at a distance of 9 or less from these two papers. I also computed the center of the largest component of the collaboration graph, and it was the set of authors in the above two papers.
What does this mean? This could mean that some of the authors of these papers are very collaborative (I know that a few of them are). This could also mean that these papers interest a greater fraction of the POPL community than most other POPL papers, either because of their subject matter or the techniques they use. Or it could be both.
At any rate, now we know the Kevin Bacons of the POPL community!
Issues and extensions
One technical issue with my method is that a few authors appear under multiple names in the DBLP database (for instance, “Nate Foster” and “J. Nathan Foster”). I don’t see an easy way to fix this. But hopefully, this problem only affects a small subset of the data.
Naturally, we could do an analysis like the above for any other CS conference, within or outside the area of PL. That’s exactly what I intend to report on over the next couple of weeks. I’ve also acquired some other data that, when cross-linked with the DBLP data, can produce some entertaining, if controversial, results. So keep an eye on this space!

Go Quakers! (Dropping my “J.” was in support of a life goal to become more like J. Gregory Morrisett. Now excuse me while I go buy some cows.)
(Complete nit-picking alert:)
Help me out here; what you wrote seems contradictory. First, you write that an overlap graph has a node for each paper with multiple authors. Later, you write that the overlap graph may be derived by coalescing maximal cliques in the collaboration graph.
Suppose that authors A&B have written a paper together, and so have B&C, and A&C, but they’ve never written one paper all together. In this case, your initial description of the overlap graph suggests that there will be three nodes, all connected (one node per paper). However, your second description suggests that these three (since they form a clique in the collaboration graph) will be considered one node.
Am I just confused?
No, you are not confused at all. The fact that you can get the overlap graph by coalescing maximal cliques in the collaboration graph is an *empirical* observation about the POPL dataset. The only relationship between the graphs that holds in general is that nodes in the overlap graph correspond to cliques (not necessarily maximal) in the collaboration graph.
Anyway, upon rereading the post, I realized that this point didn’t come out too clearly. Because the statement was confusing and wasn’t central to the main point anyway, I’ve now deleted it.
For future readers, here’s the context of this discussion. I had stated in the original version of the post that “Empirically, the overlap graph can be obtained by coalescing maximal cliques in the collaboration graph into single nodes.” For the reasons described above, I’ve now deleted this statement.
Ah! Of course. Many thanks.
From the outside, POPL looks like the theoretical PL community, but it makes sense it would have the same fragmentation issues as the other conference communities. PL just has a wide variety of topics with few connecting paradigms.
Post-conference surveys would really help here: ask participants what presentations they found interesting and what accepted papers they read or plan to read. Correlation can be done there directly (to see if there are clear subgroups and how much these groups overlap), then look at participants who are authors. One could also use such a info to identify potentially accepted duds (papers without much of an audience, though being careful that the importance of those papers might not be realized right away).
If you really want to get daring, throw in a PC member survey to see how well the PC ideas about content corresponds to the community.
I think that conflating of “co-authoring papers” and “community” isn’t quite right. For example, I’ve published on contracts with the Penn PL Club and Atsushi Igarashi… but the contracts community includes the PLT folks (Robby, Stevie, Christos, etc.), Jeremy Siek and Ron Garcia, Phil Wadler, and a few others. We’re all working on similar stuff, but I haven’t published papers with those people.
Another way to identify communities would be to analyze the way sessions are organized. Do certain authors never share sessions with other authors? I.e., do certain people always get put in an “abstract interpretation” session while others are always in “types” or “concurrency”? Unfortunately, I imagine this data is less well collated.
I’ve been meaning to do a topic analysis of POPL abstracts for a while, and I think that’s yet another way to see what the constituent communities of POPL are. (Dave and I are trying to get this done before POPL ’15, so we can present the results.)
I agree that collaboration on papers doesn’t entirely capture communities, but I also think that it’s a useful approximation.
I very much like the idea of running a topic model on abstracts, and look forward to seeing the results at POPL. Where do you get the abstracts, though? The ACM digital library?
The idea of analyzing shared sessions is excellent! But yes, I think the data would be hard to get.
To be clear: I think this is super cool, and definitely a way of understanding the communities at POPL!
And, yeah, I scraped the abstracts from the digital library, most likely in violation of some policy.
I imagine the old session schedules are up somewhere, but it would indeed be a bit of work to scrub the data.
This particular choice of example makes me a bit sad, because one of the major results of the 80s that these three areas are very closely related. Denotational semantics and type theory heavily overlap even today, but one of the reasons that Samson Abramsky’s PhD thesis (Domain Theory in Logical Form) made such a splash was because it showed how you could relate denotational semantics to abstract interpretation via Stone duality.
Briefly, domains in domain theory can be viewed as topological spaces, and their open sets can be understood as properties — indeed, as a syntactic logic. Conversely, an abstract domains can be seen as giving a language of properties, and so you can see abstract interpretation as characterizing domains with computationally-well-behaved families of open sets. David Schmidt at KSU has written some very nice recent papers explaining and elaborating on the topological aspects of abstract interpretation, and Vijay D’Silva and his coauthors have recently written a number of (IMO) really pretty papers applying these ideas to SMT.
Swarat, thanks for this post. Would you be willing to share your data and code? It would be fun to poke at it. (I’d like to understand, for example, why John Reynolds didn’t turn up in the separation logic community.)
Hi Lindsey! On your side “John Reynolds” point: That looked odd to me too. But separation logic wasn’t founded at POPL, and if we believe the ACM DL, there’s only one paper from Reynolds in those years’ POPL:
http://dl.acm.org/author_page.cfm?id=81100470240
http://dl.acm.org/citation.cfm?id=2103656.2103695
Pingback: Collaboration in PLDI and OOPSLA - The PL Enthusiast
I wrote a paper last year about identifying communities in POPL in order to generate a program committee (see http://bobbyullman.com/files/clustering/iwpaper-fall13.pdf). Similarly to Swarat, I data-mined from DBLP and analyzed the co-authorship graph. I also included edges for citations between papers (mined from CiteSeer). I played around with the relative importance of these two contributions. Overall, this approach has a variety of limitations – the most compelling is whether the model itself is valid. I believe that the model serves as good approximation, but (as has already been mentioned in the comments) topic modeling the abstract may produce more reasonable results.
Regardless, we (both Swarat and I) found that the identified clusters actually correspond to POPL communities. Even though I used a different clustering approach (stochastic block modeling using the python graph-tool library) I found similar results. Namely I identified the same Penn PL cluster. Surprisingly I do not have Peter O’Hearn as a top contributor in my one of my communities. My guess is that I tweaked parameters to more aggressively break up large clusters (producing a larger number of more highly connected components) and that Peter’s contribution was underrated by this change. In support of this conclusion I do see a cluster reminiscent of Swarat’s identified separation logic community, which in my case had Viktor Vafeiadis and Suresh Jagannathan as top contributors (also containing Matthew Fluet, Jan Vitek, Ruy Ley-Wild, Aleksandar Nanevski, and others). I’m interested in running some more experiments, but those are contingent on the logistical issues of re-installing graph-tool (the dependencies are tricky).
Stepping back a bit I don’t think these results are that surprising. As one of the biggest and most influence conferences of its type, POPL probably should be expected to draw in people from a bunch of specialized communities. One idea is that perhaps POPL should spawn specialized sub-conferences, but I would posit the cross community collaboration encourage by POPL is important. The real experiment (which I think no one should actually perform) is to replace POPL with a variety of smaller conferences and see what happens to the collaboration graph. I think (as hopefully many would agree) that this would hurt the PL community.