Expressing Security Policies

[This blog post was conceived by Steve Chong, at Harvard, and co-authored with Michael Hicks.]

Enforcing information security is increasingly important as more of our sensitive data is managed by computer systems. We would like our medical records, personal financial information, social network data, etc. to be “private,” which is to say we don’t want the wrong people looking at it. But while we might have an intuitive idea about who the “wrong people” are, if we are to build computer systems that enforce the confidentiality of our private information, we have to turn this intuition into an actionable policy.

Defining what exactly it means to “handle private information correctly” can be subtle and tricky. This is where programming language techniques can help us, by providing formal semantic models of computer systems within which we can define security policies for private information. That is, we can use formal semantics to precisely characterize what it means for a computer system to handle information in accordance with the security policies associated with sensitive information. Defining security policies is still a difficult task, but using formal semantics allows us to give security policies an unambiguous interpretation and to explicate the subtleties involved in “handling private information correctly.”

In this blog post, we’ll focus on the intuition behind some security policies for private information. We won’t dig deeply into formal semantics for policies, but we provide links to relevant technical papers at the end of the post. Later, we also briefly mention how PL techniques can help enforce policies of the sort we discuss here.

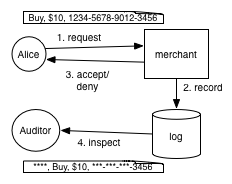
To make our discussion concrete we’ll use a running example: a system for handling credit card information. As shown in the figure, we suppose our system permits clients to submit payment requests, which the merchant either approves or denies (after consulting with the bank, not shown). A record of the transaction is stored in a log, which an auditor may later inspect. Unlike some other kinds of private information, we’re lucky here in that there is an industry standard that describes how credit card information should be handled: the Payment Card Industry Data Security Standard (PCI DSS). We’ll focus on what the standard says about the privacy of logs that our application may generate.[ref]Privacy of logging is PCI DSS requirement 3.4.[/ref]

Noninterference

What security policy would be suitable for the credit card information? We might be tempted to use a noninterference security policy. Mike described noninterference in an earlier blog post. In a nutshell, noninterference requires that public outputs do not on depend private inputs. More formally, if we think of our system as a function that takes some private and public inputs and produces public output, then we can express noninterference as follows:

For all public inputs L and any pair of private inputs H1 and H2, we have: if S(H1,L) = O1 and S(H2,L) = O2 then O1 = O2.

Here, we regard the credit card information as private inputs and our application log as public output.[ref]The application log is not public in the sense that not everyone can see the log. However, more people can see the application log than should be allowed to see the credit card information. So the application log is *more public* than the credit card information. For simplicity in this post we will consider just two privacy levels: private and public. But noninterference (and the other security guarantees and policies described here) can be generalized to more than just two privacy levels.[/ref] Noninterference intuitively means someone who looks at the application log (the public output) doesn’t learn anything about the credit cards our application has used (the private inputs).

Assessing noninterference as a policy

Noninterference has a lot going for it:

• Noninterference is a simple security guarantee with a clear threat model: the adversary can observe some of the execution (the public outputs) of a system whose internal workings we assume he knows; the goal is to nevertheless prevent him from learning anything about the private inputs.

• Noninterference is an extensional guarantee: it is defined in terms of the input/output behavior of a computer system, not with details of how the system is implemented. If a system satisfies noninterference, then a different implementation of the system with the exact same behavior would also also satisfy noninterference.

• Noninterference is flexible in scope: By carefully choosing what we regard as “private inputs” and “public outputs”, we can model different systems and adversaries. For example, we might regard the pattern of memory accesses as a public output, and noninterference would require that private information isn’t revealed through that particular channel.

Note that these benefits of noninterference are due in large part to using a formal semantics as a model for computer systems. A formal statement of noninterference (like the one above) is typically simple, is based on the extensional semantics of a program, and clarifies assumptions on what the adversary knows and can observe.

Noninterference is a kind of information-flow guarantee, as it characterizes what flows of information are permitted in a system. In particular, noninterference does not allow any information to flow from private inputs to public outputs, but allows all other information flows.

Noninterference is too strong for credit card example

Unfortunately, noninterference doesn’t hold for our credit card application because we may want to record some information about credit cards in our log. For example, we might store the last four digits of a transaction’s card to help determine, on audit, which card was used. Or, more interestingly, maybe our application uses multiple payment gateways. The log should record which payment gateway was used because the choice depends on the type of the credit card. In both examples, our application violates noninterference: the public contents of the log depend on private credit card information.

Declassification

The issue for our credit card application is that we need to release, or declassify, some (but not all) of the credit card information. Partial, or circumstantial, declassification is common in systems that handle private information. For example, a patient’s medical records are normally private, but may be released under certain circumstances, such as when a physician is consulting on the case, or when the patient has signed an appropriate information release authorization form, as required under legislation such as HIPAA. Or, another example: the individual salaries of employees are private, but the average salary of all employees may be released.

The challenge is to be able to define security policies that can express what it means to declassify private information appropriately. That is, what information is ok to release? Under what circumstances? To whom? As with noninterference, the use of formal semantics for computer systems can help us to clearly and unambiguously define what it means for a computer system to handle information in accordance with declassification policies.

Declassification in credit card example

For our credit card application, PCI DSS describes what can be declassified (or, at least, what is permitted to be stored in the log). It allows us to declassify up to the first six and last four digits of the credit card number.[ref]The PCI DSS also permits other declassifications of private credit card information, including hashes and encryptions of credit card numbers.[/ref]

We can adapt our semantic definition of noninterference to account for declassification. If we have two executions of the system that have the same public inputs but different private inputs (i.e., different credit card numbers) then the public output (i.e., the application log) will likely be different for each execution, since the last four and/or first six digits of the credit card numbers will likely be different. But intuitively, we want our declassification policy to capture the idea that the public output doesn’t reveal anything more than the last four and/or first six digits. We can capture that with the following definition, which says that if we have two executions where the private inputs have the same last four and first six digits, but may differ arbitrarily for the remaining digits, then the public output is the same.

For all public inputs L and any pair of private inputs H1 and H2 such that firstFour(H1) = firstFour(H2) and lastSix(H1) = lastSix(H2), we have: if S(H1,L) = O1 and S(H2,L) = O2 then O1 = O2.

Erasure

Declassification makes information less private, and in our application, we needed a declassification policy to describe “correct handling” of the private credit card information.

However, declassification policies alone are not sufficient to describe “correct handling” of credit cards: the PCI DSS also requires that information should be made more private. More precisely, it requires that sensitive authentication data (such as the CVC2 number on the back of a card) should not be stored after the credit card transaction has been authorized.

Many other systems also need to make information more private during execution. This is called information erasure, since typically the information becomes so private that it should be removed from the system. But we can generalize this to allow information to remain in the system, but with more restrictions on its use. Examples of erasure include: at the end of a private browsing session, a web browser needs to erase information about the websites visited during the session; a course management system needs to make assignment solutions unavailable when the course ends (although course staff may still access them).

Information erasure requires not just removing the private data, but also data derived from the private data. That is, there is a distinction between information erasure and data deletion: a system may delete private data, but still reveal information derived from the data, and thus violate information erasure. Conversely, a system can satisfy information erasure and still have the private data exist on the system provided that the public outputs reveal nothing about the erased information.

Erasure and data deletion in credit card example

The PCI DSS requirements are phrased in terms “not storing” sensitive data after authorization, and likely the authors had data deletion in mind. However, suppose our application derived some information from the CVC2 number. For example, suppose the application determined whether the CVC2 number was even or odd, and kept (and output) that information in the system after authorization, despite removing everything else about the CVC2 number from the system. Our application would satisfy the deletion of the CVC2 number, but would not satisfy the information erasure of the CVC2 number. Revealing information that is derived from or dependent on the CVC2 number after authorization is A Bad Thing, and so our application should enforce both information erasure and data deletion of the sensitive authentication data.

We can develop a noninterference-like formal specification of erasure policies. However, the model of the system needs to be a bit different than the model we used above for noninterference and declassification policies. Since the requirement is that after the transaction the CVC2 number is not stored, we would use public outputs to model the system’s storage. Also, we would need to be able to talk about the storage throughout the execution, rather than just at the end of the execution, since it is fine for the CVC2 number to be stored before authorization and should be removed once the transaction has been authorized. Although we skip giving a formal definition here, the key point is that formal PL semantics allow us to precisely state what erasure means.

More and more security requirements?

There are other information security requirements that we could consider. In addition to personal private information, we may be concerned more generally with the confidentiality of information (e.g., trade secrets, a company’s financial reports, military intelligence). Integrity is a well-known dual to confidentiality, which speaks about the trustworthiness of data. The ideas of noninterference, declassification, and erasure that we have explored for privacy apply more generally to confidential information and have analogues for integrity. But we could also extend our specification of “correct handling” of sensitive information to consider, for example, the interaction of integrity and confidentiality requirements, or the relationship of information-flow security policies with other security mechanisms such as authorization, authentication, and audit.

Balancing extensional and intensional definitions

We could imagine further refining security policies, pushing them to include more and more of the functional specification of a system. But this would lose much of the value of expressive security policies, which is to form a concise summary of the information security of a system.

This is a fine line to walk: if we include more of the functional specification in the security policies, then the information security of the system is more tightly specified but the security policies are more complex. And the more complex the security policies, the greater the likelihood of them being wrong with respect to the actual security requirements of the system. Conversely, if we include less of the functional specification in the security policies, then the policies are simpler, but perhaps they fail to adequately express the actual security requirements of the system. We see the same tension in precise type systems.

Where exactly this line falls is not yet clear. However, this is an active area of research, with a number of researchers exploring simple yet expressive security policies with clear semantic guarantees, and efficient light-weight enforcement mechanisms. We are optimistic that we can drive down the costs of specifying and enforcing expressive security policies to the point where they are outweighed by the benefits of strong and expressive information security guarantees.

PL for definition, PL for enforcement

In this post we have focused on the definition of security policies, using PL semantics to help. Once we have a clear definition of security policies, we can think about how to ensure that a system actually enforces those policies on private information. PL techniques can help us here too! In general, there are a variety of ways we can enforce security policies. PL mechanisms—such as type systems, formal verification, and/or dynamic analysis—can all be used to enforce many kinds of security policies. We will leave discussion of these things to a future post.

Further reading

For a great (though somewhat dated) survey on noninterference and information-flow security, see “Language-based information-flow security” by Andrei Sabelfeld and Andrew Myers [1].

There are a number of ways to characterize declassification. According to the taxonomy given by Andrei Sabelfeld and David Sands [2], declassification policies are often concerned with what information is permitted to be declassified, when (under what conditions) information can be declassified, who can authorize declassification and be affected by it, where in the system (i.e., which components) can declassify information, and which security levels declassification is permitted between. Researchers have explored various combinations of these four aspects of declassification, but determining which style of declassification policy to use typically depends on the application at hand. That is, for some applications, the important aspect is what information is declassified, whereas for other applications, the important aspect is when information is declassified.

A noninterference-based notion of information erasure was introduced by Steve Chong and Andrew Myers [3]. Aspects of declassification also have analogies for erasure. Thus, we may want security policies that characterize what information needs to be erased, when that information should be erased, and so on. For our application with credit card data, the important aspects are when information should be erased (i.e., at the time of authorization), and what should be erased (i.e., sensitive authentication data).

[1] Sabelfeld, A. and A. C. Myers (2003, January). Language-based information-flow security. IEEE Journal on Selected Areas in Communications 21(1), 5-19.

[2] Sabelfeld, A. and D. Sands (2005, June). Dimensions and principles of declassification. In Proceedings of the 18th IEEE Computer Security Foundations Workshop, pp. 255-269. IEEE Computer Society.

[3] Chong, S. and A. C. Myers (2005, June). Language-based information erasure. In Proceedings of the 18th IEEE Computer Security Foundations Workshop, pp. 241-254. IEEE Computer Society.